Page 47 - LC-SFC_Pharma_Brochure

C191-E042

4. Data Analysis Using LabSolutions 5. Conclusion
Data Analysis Using LabSolutions
5. Conclusion
4.
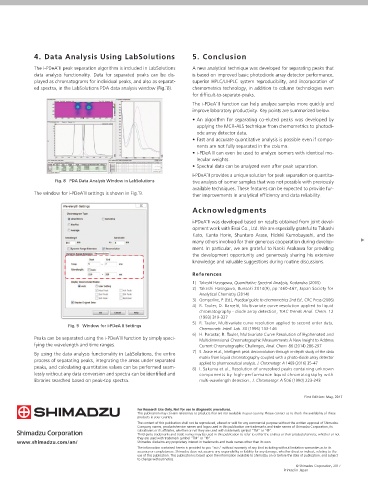
The i-PDeA˜II peak separation algorithm is included in LabSolutions A new analytical technique was developed for separating peaks that New Data Processing Method for
data analysis functionality. Data for separated peaks can be dis- is based on improved basic photodiode array detector performance,
played as chromatograms for individual peaks, and also as separat- superior HPLC/UHPLC system reproducibility, and incorporation of Technical Photodiode Array Detectors
ed spectra, in the LabSolutions PDA data analysis window (Fig.˜8). chemometrics technology, in addition to column technologies even
for difficult-to-separate-peaks. Report Principle and Overview of Intelligent Peak Deconvolution
The i-PDeA˜II function can help analyze samples more quickly and Analysis (i-PDeA II)
improve laboratory productivity. Key points are summarized below.
• An algorithm for separating co-eluted peaks was developed by Toshinobu Yanagisawa 1
applying the MCR-ALS technique from chemometrics to photodi-
ode array detector data.
• Fast and accurate quantitative analysis is possible even if compo-
nents are not fully separated in the column. Abstract:
• i-PDeA II can even be used to analyze isomers with identical mo- An i-PDeA II (Intelligent Peak Deconvolution Analysis II) data analysis technique was developed for extracting target peaks from unsepa-
lecular weights. rated peaks by analyzing photodiode array (PDA) detector data using the chemometrics multivariate curve resolution alternating least
• Spectral data can be analyzed even after peak separation. squares (MCR-ALS) technique. The i-PDeA˜ II function can separate peaks for multiple components in absorption spectra and chromato-
i-PDeA˜II provides a unique solution for peak separation or quantita- grams by simply specifying the wavelength and time ranges. The i-PDeA˜II function can be used to identify spectra and quantitate peaks
Fig. 8 PDA Data Analysis Window in LabSolutions tive analysis of isomer samples that was not possible with previously after separation of individual components, even for difÿcult-to-separate peaks for which a standard sample cannot be prepared. Further-
available techniques. These features can be expected to provide fur- more, because i-PDeA˜II separates peaks based only on differences in spectral shape, it can also be used to separate and quantitate peaks
The window for i-PDeA˜II settings is shown in Fig.˜9. ther improvements in analytical efficiency and data reliability. for co-eluted isomers. This report explains the principle used by the i-PDeA˜II technique to separate peaks, describes an example of using
i-PDeA˜II to analyze a sample with isomers of three components, and evaluates the spectral identiÿcation and quantitation performance.

Acknowledgments Keywords: Photodiode array detector, chemometrics, MCR-ALS, and LabSolutions
Acknowledgments
i-PDeA˜II was developed based on results obtained from joint devel-
opment work with Eisai Co., Ltd. We are especially grateful to Takashi
Kato, Kanta Horie, Shuntaro Arase, Hideki Kumobayashi, and the
1.
Fundamental Theor
etical Basis
many others involved for their generous cooperation during develop- 1. Fundamental Theoretical Basis where,
for Peak Deconvolution Algorithm
ment. In particular, we are grateful to Naoki Asakawa for providing for Peak Deconvolution Algorithm d(t 1 ,λ 1 ) ... d(t 1 ,λ m ) α 1 β 1 γ 1
the development opportunity and generously sharing his extensive D = … ... … , c 1 = … , c 2 = … , c 3 = …
knowledge and valuable suggestions during routine discussions. 1-1. Modeling PDA Detector Data d(t n ,λ 1 ) ... d(t n ,λ m ) α n β n γ n
α 1 β 1 γ 1 s 1 (λ 1 ) ... s 1 (λ m )
Given peak profiles and spectra for each component in a three-com- C = , S = s 2 (λ 1 ) ... s 2 (λ m )
T
References … … …
ponent mixture, c1(t), s1(λ), c2(t), s2(λ), c3(t), and s3(λ), then measure- α n β n γ n s 3 (λ 1 ) ... s 3 (λ m )
1) Takeshi Hasegawa, Quantitative Spectral Analysis, Kodansha (2005) ment data in an ideal system d(t,λ) can be described by the following
2) Takeshi Hasegawa, Bunseki 2014(9), pp.˜460-467, Japan Society for Measurement data Peak pro les Spectra
Analytical Chemistry (2014) expression. d(t, λ) s2
3) Gemperline, P. (Ed.), Practical guide to chemometrics 2nd Ed., CRC Press (2006) d(t,λ) = c 1 (t)s 1 (λ) + c 2 (t)s 2 (λ) + c 3 (t)s 3 (λ)
4) R. Tauler, D. Barceló, Multivariate curve resolution applied to liquid Then spectra d(ti,λ) measured as a function of time ti can be expressed s3
chromatography - diode array detection, TrAC Trends Anal. Chem. 12 as follows: s1
(1993) 319-327 c1 c2 c3
5) R. Tauler, Multivariate curve resolution applied to second order data, d(t i ,λ) = c 1 (t i )s 1 (λ) + c 2 (t i )s 2 (λ) + c 3 (t i )s 3 (λ) Wavelength
Fig. 9 Window for i-PDeA II Settings Retention time
Chemometr. Intell. Lab. 30 (1995) 133-146 Assuming spectral components are vectors with discrete values λj Retention time Wavelength
6) H. Parastar, R. Tauler, Multivariate Curve Resolution of Hyphenated and Deconvolute to individual component
Peaks can be separated using the i-PDeA˜II function by simply speci- Multidimensional Chromatographic Measurements:A New Insight to Address (where j˜=˜1 to m), then spectra can be described as follows:
fying the wavelength and time ranges. Current Chromatographic Challenges, Anal. Chem. 86 (2014) 286-297 T T T T s 1 T T c1(t)s1(λ) c2(t)s2(λ) c3(t)s3(λ)
By using the data analysis functionality in LabSolutions, the entire 7) S. Arase et al., Intelligent peak deconvolution through in-depth study of the data d i = α i s 1 + β i s 2 + γ i s 3 = (α i β i γ i ) s 2 T
process of separating peaks, integrating the areas under separated matrix from liquid chromatography coupled with a photo-diode array detector where, s 3
applied to pharmaceutical analysis, J. Chromatogr. A 1469 (2016) 35–47
peaks, and calculating quantitative values can be performed seam- 8) I. Sakuma et al., Resolution of unresolved peaks containing unknown d i = (d(t i ,λ 1 ) ... d(t i ,λ m ))
T
lessly without any data conversion and spectra can be identified and components by high-performance liquid chromatography with α i = c 1 (t i ), β i = c 2 (t i ), γ i = c 3 (t i ) Wavelength Retention time Wavelength Retention time Wavelength Retention time
libraries searched based on peak-top spectra. multi-wavelength detection., J. Chromatogr. A 506 (1990) 223-243
T
T
T
s 1 = (s 1 (λ 1 ) ... s 1 (λ m )), s 2 = (s 2 (λ 1 ) ... s 2 (λ m )), s 3 = (s 3 (λ 1 ) ... s 3 (λ m )) Fig. 1 Measurement Data from Three-Component Mixture Sample
By summarizing each spectrum measurement at time ti (where i˜=˜1
First Edition: May, 2017 The data can be expressed schematically as follows:
to n), measurements can be expressed in matrix form, as follows:
T T
d 1 α 1 β 1 γ 1 s 1
= … … … s 2 T Meaurement spectrum 1 Component 1 pure spectrum
…
T T … = Component 1 profile Component 2 profile Component 3 profile Component 2 pure spectrum
d n α n β n γ n s 3
Meaurement spectrum n Component 3 pure spectrum
or by direct product (outer product), as follows:
T T T
D = c 1 s 1 + c 2 s 2 + c 3 s 3 Eq.˜(1)
or alternatively Considering measurement error, noise, and unpredictable factors, and
1), 2)
D = CS T Eq.˜(2) given a remainder R, the measurement data can be modeled as follows:
D = CS + R
T
This relational expression is valid for any number of components.
© Shimadzu Corporation, 2017 1 Analytical & Measuring Instruments Division 1
Printed in Japan