Page 12 - Oligonucleotide Therapeutics Solution Guide

Characteristic analysis
Quality Control

Thermodynamic Parameter Analysis UV-2600i+TMSPC-8

Activity Index for Oligonucleotide Therapeutics
Tm Analysis and Thermodynamic Characterization ~ Thermodynamic Parameter Analysis ~

of Oligonucleotide Therapeutics The Gibbs free energy is an indicator of the activity of oligonucleotide therapeutics. Modification Target selection
click here The Gibbs free energy is the non-expanding work, which represents the maximum work used for binding between strands in oligonucleotides.
The higher the negative value, the stronger the binding force of the strands.

• The Tm can be used to determine the amount of change in the Gibbs free The Gibbs free energy change is described thermodynamically and statistically by the following equation
energy, an index of drug activity.
• Users get thermodynamic properties like entropy and enthalpy. ∆G = ∆H －T∆S (1)
benefits • Equipped with eight microcells, users can efficiently measure and analyze ∆G = ∆G̊ ＋ RTlnK (2)
∆G = ∆H －T∆S
(1)
a large number of samples. ∆G = ∆G̊ ＋ RTlnK (2) Unprotected Excision
∆G = ∆H －T∆S
(1)
where K is the equilibrium constant, R is the gas constant, and Δ G ° is the standard Gibbs free energy. Oligomer synthesis
∆G = ∆H －T∆S
When considering the equilibrium constant of a oligonucleotide, the oligonucleotide can be described as an equilibrium reaction between two
∆G = ∆G̊ ＋ RTlnK
(2)
Methods and Results 2 molecules in which sense chain A and antisense chain B are associated in a 1:1 ratio. (1)
∆G = ∆H －T∆S
A＋B ↔ AB
(1)
1.8 60 µM ∆G = ∆G̊ ＋ RTlnK (3)
(2)
Sample M13 primer 1.6 ∆G = ∆G̊ ＋ RTlnK (2)
Forward 5’-CGACGTTGTAAAACGACGGCCAGGA-3’ A＋B ↔ AB (3)
Reverse 5‘-TCCTGGCCGTCGTTTTACAACGTCG-3’ 1.4 40 µM
Conc., Volume 2, 5, 9, 12, 20, 40, 60 µmol/L 1.2 2 α
K ＝
2, 5 µmol/L :100 µL in a cell of 10 mm optical path length Absorbance 1 A＋B ↔ AB (3)
(4)
c ( 1－ α) 2
9 ~ 60 µmol/L :10 µL in a cell of 1 mm optical path length The double-stranded state mole fraction is denoted by α, and the total concentration of oligonucleotide is denoted by C. Because the concentrations
2 α
K ＝
Preparation Samples are prepared to the above concentrations using 66.7 0.8 20 µM A＋B ↔ AB (3)
A＋B ↔ AB
(4) (3)
mmol/L phosphate buffer containing 5 mol/L NaCl. Samples are 0.6 12 µM of A and B [A] and [B] at complete dissociation are C/2, the equilibrium constant can be expressed as:
c ( 1－ α) 2
then annealed by mixing equal amounts of Forward and Reverse, 0.4 Purification
warming at 95 °C for more than 10 minutes, and cooling. 2 α
0.2 K ＝ 4
c ( 1－ α
Analytical As shown in Table 1 9 µM ∆G̊ = RT ln (4)
2 α
Conditions 0 K ＝ 2 α m ) 2 c (5)
40 50 60 70 80 (4)
K ＝
c ( 1－ α) 2
Results We measured Tm for seven samples of different concentrations, ∆G̊ = RT ln 4 (4)
m ) 2
and determined enthalpy change ΔH̊, entropy change ΔS̊, and c ( 1－ α c (5)
Gibbs free energy change ΔG̊. Temperature (˚C)
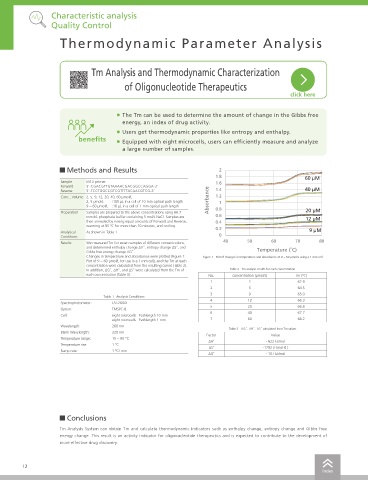
Changes in temperature and absorbance were plotted (Figure 1: Figure 1 Plot of changes in temperature and absorbance at 9 ~ 60 μmol/L using a 1 mm cell It is in equilibrium when the temperature is Tm. And α = 1/2 and ΔG = 0, the equation (2) is expressed as follows.
4
R
Plot of 9 ~ 60 μmol/L for use in a 1 mm cell), and the Tm at each 1 ∆G̊ = RT ln 4 ∆S̊ (5)
m
concentration were calculated from the resulting curves (Table 2). = － ln c c 4 ＋
∆G̊ = RT ln 4
In addition, ΔG̊, ΔH̊, and ΔS̊ were calculated from the Tm of Table 2 Tm analysis results for each concentration T m ∆H̊ ∆H̊ (5)
R m
1
= －
each concentration (Table 3). No. concentration (µmol/L) Tm (°C) ∆G̊ = RT ln 4 c ＋ ∆S̊ (5)
m
c ln c
∆S̊
R
c
ln
1 2 62.9 T m = ∆H̊ ∆H̊ 4 ＋ ∆H̊ ∆H̊
2 5 64.5 1 R R c 4 ∆S̊∆S̊
ln ln
= = －
ΔG° is the standard Gibbs free energy at 1 atm and 25 °C. Substituting expression (5) into expression (1) yields, the following relational expression:.
3 9 65.0 ＋ ＋
∆S̊
Table 1 Analysis Conditions T m ∆H̊ ∆H̊ 4 c ∆H̊ ∆H̊ Quality Control
4
R
1
4 12 66.3 = －
1
Spectrophotometer: UV-2600i T m = － R ln 4 ＋ ∆S̊ Characteristic analysis
R ∆H̊ ln
c c ＋
ln
5 20 66.8 ∆S̊∆H̊
Option: TMSPC-8 T m = ∆H̊ ＋ c ∆H̊
6 40 67.7 ∆H̊ 4 c ∆H̊
∆S̊
Cell: eight microcells Pathlength 10 mm = R ln c ＋ ∆S̊
R
eight microcells Pathlength 1 mm 7 60 68.2 = ∆H̊ ln 4 ＋ ∆H̊
Wavelength: 260 nm ∆H̊ 4 ∆H̊
Table 3 ΔG̊, ΔH̊, ΔS̊ calculated from Tm values
Blank Wavelength: 320 nm
Factor Value
Temperature range: 15 ~ 90 °C
ΔH˚ - 622 kJ/mol
Temperature rise: 1 °C Based on the above, the enthalpy change ΔH ° of the standard state is determined from the slope of the straight line obtained by plotting the
ΔS˚ -1792 J/ (mol∙K )
Ramp rate: 1 °C/ min reciprocal of the Tm value (1/Tm) on the vertical axis and ln (C/4) on the horizontal axis, and the entropy change ΔS° of the standard state is DDS
ΔG˚ - 107 kJ/mol
determined from this slope and the y intercept.
Therefore, to determine ΔH° and ΔS° in duplex formation, it is necessary to prepare samples of various concentrations (C), determine the Tm of Pharmacokinetics
each sample, and plot 1/Tm against ln (C/4).
The Tm analysis software can calculate the Tm value for each concentration.
When analyzing by this method, the oligonucleotide concentration (C) should be as wide as possible (several tens of times or more). The
combination of cells with optical path lengths of 10 mm and 1 mm makes it possible to measure data over a wide range of concentrations. In
Conclusions addition, the minimum required sample volume is 10 μL, which can be measured in small amounts.
Other
Tm Analysis System can obtain Tm and calculate thermodynamic indicators such as enthalpy change, entropy change and Gibbs free In addition to the Gibbs free energy change ΔG°, which indicates the strength of binding force, the user can also know which function is
energy change. This result is an activity indicator for oligonucleotide therapeutics and is expected to contribute to the development of dominant, which enables more effective drug discovery.
more effective drug discovery.
12 13
index index